
Page 11 A New Quantitative Approach to All Information
REVERSE

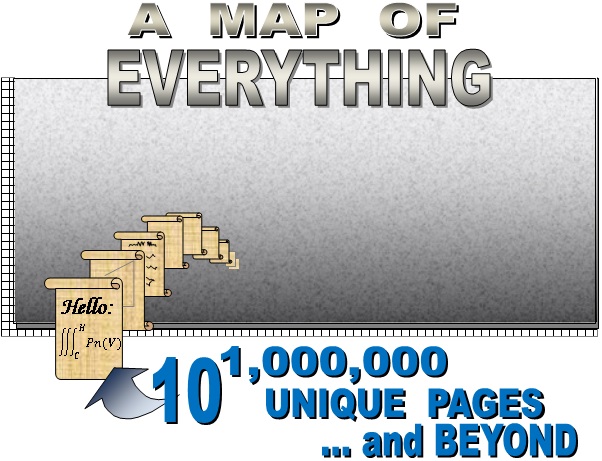


Page 4 How many unique strandard-sized pages of writings and drawings can you produce? Ans: Some 10million pages.
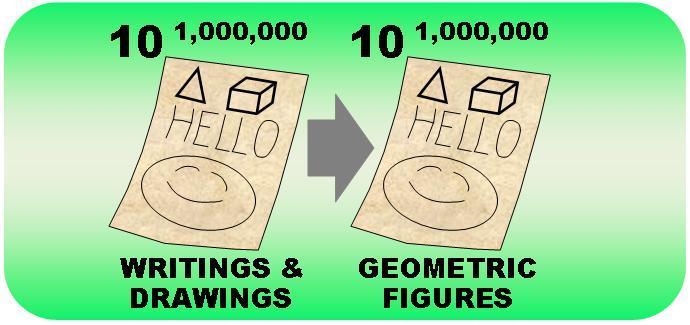
Page 5 A mega-digit number of geometrical figures.
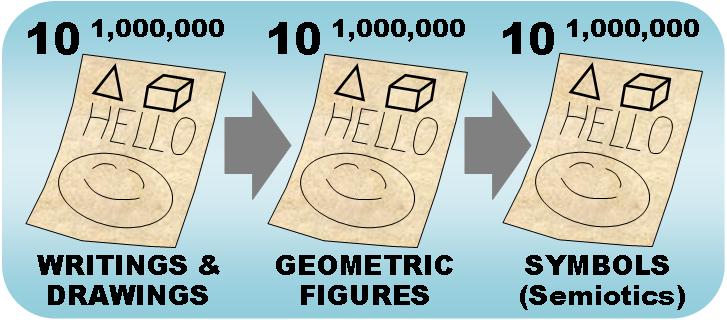
Page 6 A mega-digit number of symbols.
Page 7 A mega-digit number of pages of unique information.

Page 8 Constructing the Grand Map of Everything.
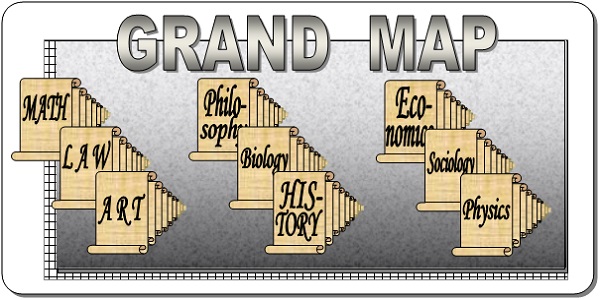
Page 9 Essentially Every Academic Subject Represented
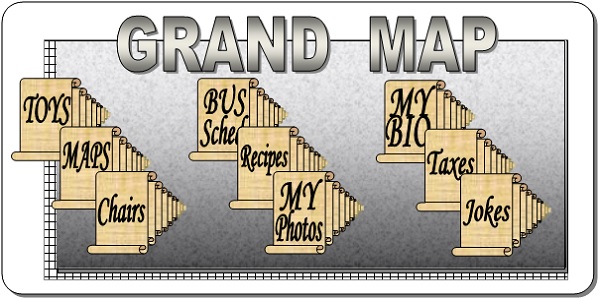
Page 10 Essentially Every Non-Academic Subject Represented

Page 11 A New Quantitative Approach to All Information
Page 220 Chapter: "INFINITE BUTTERFLIES"
Mapping Information of the Universe onto Butterfly Wings
Page 220.1 How many unique butterflies do you need to get the complete works of Shakespeare?

Page 220.2 A Small Book About The BIG EVERYTHING.

Page 220.3
Page 301.1 Commentary Section.

Page 520.102 The foundation starts with defining a mathematical object called a PAGE.

Page 520.105 Building grand geometric objects out of pages.